归并排序是分治算法的一个典型应用实例,大致实现原理是:
分解
先把待排序的序列拆分为上下两个数组,然后把每一半再拆分为两半,重复这个步骤,直到拆分为length个单个元素的数组。
合并
再进行两两合并:把每两个数组合并成一个排序好的数组,重复这个步骤,1合2,2合4(合不了2就合1,合不了4就和3,以此类推)...,最后得到的就是一个排序好的序列。
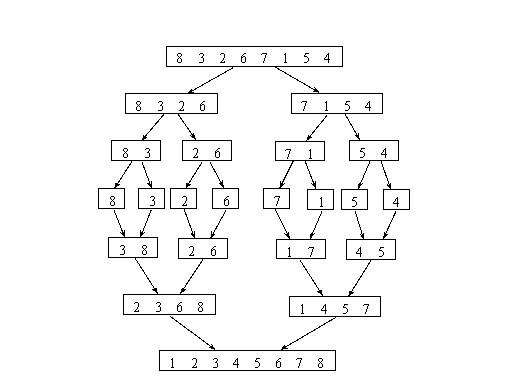 图片源自百度
图片源自百度
代码实现:
include
using namespace std;
//再把两半排好序的数组组合排成一个新的排好序的数组
void func2(int a[],int begin,int m,int end,int tmp[]){
int p = 0; //做存放进tmp时的下标
int p1 = begin,p2 = m+1; //分别代表每半数组的下标
//只要有其中一半数组走到头了,就跳出
while(p1<=m&&p2<=end){
if(a[p1]<a[p2]) tmp[p++] = a[p1++];
else tmp[p++] = a[p2++];
}
//然后如果哪半有剩余,就把哪半依次装进tmp数组
while(p1<=m)
tmp[p++] = a[p1++];
while(p2<=end)
tmp[p++] = a[p2++];
//最后把tmp数组元素拷贝进原数组a
for(int i = 0;i < (end-begin+1);i++)
a[begin+i] = tmp[i];
}
//先把要排序的数组两两拆开
void func1(int a[],int begin,int end,int tmp[]){
if(begin<end){
int m = begin+(end-begin)/2;
func1(a,begin,m,tmp); //左半部分继续分
func1(a,m+1,end,tmp); //右半部分继续分
//直到分到begin>=end,即只有一个元素时,就开始合并
func2(a,begin,m,end,tmp);
}
}
int main(){
int a[10] = {3,7,1,6,9,0,8,2,5,4};
int b[10]; //备用数组
func1(a,0,9,b);
for(int i = 0;i < 10;i++)
printf("%d ",a[i]);
printf("\n");
return 0;
}上面的写法可以方便理解,一个函数负责分解,一个函数负责合并,而实际应用中这两个函数可以合并在一起。
源码如下:
#include<iostream>
#include<cstring>
using namespace std;
//归并排序
void margeSort(int arr[],int begin,int end){
if(begin==end)return;
int mid = (begin+end)/2;
margeSort(arr,begin,mid);margeSort(arr,mid+1,end);
int tmp[end-begin],idx = begin,ln = begin,rn = mid+1;
while(ln<=mid&&rn<=end){
if(arr[ln]<=arr[rn])tmp[idx++] = arr[ln++];
else tmp[idx++] = arr[rn++];
}
while(ln<=mid){tmp[idx++] = arr[ln++];}
while(rn<=end){tmp[idx++] = arr[rn++];}
for(int i = begin;i<=end;i++)arr[i] = tmp[i];
}
int main(){
int arr[10] = {3,7,1,6,9,0,8,2,5,4};
margeSort(arr,0,sizeof(arr)/sizeof(*arr)-1);
for(int num:arr)
cout << num << " ";
cout << endl;
return 0;
}时间复杂度:
归并排序是一种稳定的排序方法(前提是相等时先放左边的数),
| 最好情况 | 最坏情况 | 平均 |
|---|---|---|
| O(nlogn) | O(nlogn) | O(nlogn) |
空间复杂度:
像第一种用一个等长tmp数组做临时存放工作的函数,因为所有临时存放工作都是在tmp中完成,所以空间复杂度为O(n)。
而第二种函数,因为每次合并都需要申请一次和待合并等长的数组做临时存放工作,所以空间复杂度为O(logn)。