1. 公因子的数目

给你两个正整数 a 和 b ，返回 a 和 b 的 公 因子的数目。

如果 x 可以同时整除 a 和 b ，则认为 x 是 a 和 b 的一个 公因子 。

示例 1：

输入：a = 12, b = 6
输出：4
解释：12 和 6 的公因子是 1、2、3、6 。

示例 2：

输入：a = 25, b = 30
输出：2
解释：25 和 30 的公因子是 1、5 。

思路

数据范围比较小，直接暴力即可。

代码

class Solution {
public:
    int commonFactors(int a, int b) {
        int n = 0;
        for(int i = 1;i <= min(a, b);i++){
            if(a %i == 0 && b % i == 0)n++;
        }
        return n;
    }
};

2. 沙漏的最大总和

给你一个大小为 m x n 的整数矩阵 grid 。

按以下形式将矩阵的一部分定义为一个 沙漏 ：


返回沙漏中元素的 最大 总和。

注意： 沙漏无法旋转且必须整个包含在矩阵中。

示例 1：

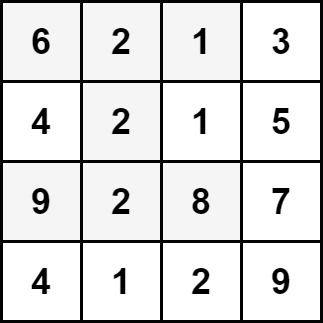
输入：grid = [[6,2,1,3],[4,2,1,5],[9,2,8,7],[4,1,2,9]]
输出：30
解释：上图中的单元格表示元素总和最大的沙漏：6 + 2 + 1 + 2 + 9 + 2 + 8 = 30 。

示例 2：

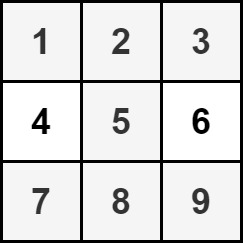
输入：grid = [[1,2,3],[4,5,6],[7,8,9]]
输出：35
解释：上图中的单元格表示元素总和最大的沙漏：1 + 2 + 3 + 5 + 7 + 8 + 9 = 35 。

提示：

  • m == grid.length
  • n == grid[i].length
  • 3 <= m, n <= 150
  • 0 <= grid[i][j] <= $10^6$

思路

暴力

代码

class Solution {
public:
    int maxSum(vector<vector<int>>& grid) {
        int maxn = INT_MIN;
        int ia[] = {-1, -1, -1, 0, 1, 1,1};
        int ja[] = {-1, 0, 1, 0, -1, 0, 1};
        for(int i = 1;i < grid.size() - 1;i++){
            for(int j = 1;j < grid[0].size() - 1;j++){
                int cmaxn = 0;
                for(int t = 0;t <7;t++){
                    cmaxn += grid[i + ia[t]][j + ja[t]];
                }
                maxn = max(maxn, cmaxn);
            }
        }

        return maxn;
    }
};

3. 最小 XOR

给你两个正整数 num1 和 num2 ，找出满足下述条件的整数 x ：

  • x 的置位数和 num2 相同，且
  • x XOR num1 的值 最小

注意 XOR 是按位异或运算。

返回整数 x 。题目保证，对于生成的测试用例， x 是 唯一确定 的。

整数的 置位数 是其二进制表示中 1 的数目。

示例 1：

输入：num1 = 3, num2 = 5
输出：3
解释：
num1 和 num2 的二进制表示分别是 0011 和 0101 。
整数 3 的置位数与 num2 相同，且 3 XOR 3 = 0 是最小的。

示例 2：

输入：num1 = 1, num2 = 12
输出：3
解释：
num1 和 num2 的二进制表示分别是 0001 和 1100 。
整数 3 的置位数与 num2 相同，且 3 XOR 1 = 2 是最小的。

提示：

  • 1 <= num1, num2 <= $10^9$

思路

挺有意思的一道位运算贪心题，首先计算num2的二进制中1的bit位数，对应x的bit为1的位数，然后要和num1异或值最小，那么就让x从高位往低位按照num1的1bit位填1，如果num2的1bit位数比num1更多，多的就让x从低位往高位把0bit填1，最后的x即为结果。
例如num1 = 8， num2 = 5:
num2的二进制为：0101
两个1所以求得x的1bit位有2个
num1的二进制为：1000
x从高位往前对应num1填两个1，但num1只有1个1bit，所以多余的从低位往前填，结果为：
x 二进制为： 1001,所以输出十进制9。

代码

class Solution {
public:
    int minimizeXor(int num1, int num2) {
        int bn = 0;
        for(int i = 0;i < 32;i++){
            if((num2 >> i) & 1)bn++;
        }
        int num = 0;
        for(int i = 31;i >= 0 && bn > 0;i--){
            if((num1 >> i) & 1){
                num += 1 << i;
                bn--;
            }
        }
        for(int i = 0;i < 32 && bn > 0;i++){
            if(((num >> i) & 1) == 0){
                bn--;
                num += 1 << i;
            }
        }

        return num;
    }
};

4. 对字母串可执行的最大删除数

给你一个仅由小写英文字母组成的字符串 s 。在一步操作中，你可以：

  • 删除 整个字符串 s ，或者
  • 对于满足 1 <= i <= s.length / 2 的任意 i ，如果 s 中的 前 i 个字母和接下来的 i 个字母 相等 ，删除 前 i 个字母。

例如，如果 s = "ababc" ，那么在一步操作中，你可以删除 s 的前两个字母得到 "abc" ，因为 s 的前两个字母和接下来的两个字母都等于 "ab" 。

返回删除 s 所需的最大操作数。

示例 1：

输入：s = "abcabcdabc"
输出：2
解释：
- 删除前 3 个字母（"abc"），因为它们和接下来 3 个字母相等。现在，s = "abcdabc"。
- 删除全部字母。
一共用了 2 步操作，所以返回 2 。可以证明 2 是所需的最大操作数。
注意，在第二步操作中无法再次删除 "abc" ，因为 "abc" 的下一次出现并不是位于接下来的 3 个字母。

示例 2：

输入：s = "aaabaab"
输出：4
解释：
- 删除第一个字母（"a"），因为它和接下来的字母相等。现在，s = "aabaab"。
- 删除前 3 个字母（"aab"），因为它们和接下来 3 个字母相等。现在，s = "aab"。 
- 删除第一个字母（"a"），因为它和接下来的字母相等。现在，s = "ab"。
- 删除全部字母。
一共用了 4 步操作，所以返回 4 。可以证明 4 是所需的最大操作数。

示例 3：

输入：s = "aaaaa"
输出：5
解释：在每一步操作中，都可以仅删除 s 的第一个字母。

思路

先找规律，例如：串s为：'abab'，对于这个串开头前两个ab和后两个相同，所以可以删除开头ab。
那么串s的最大操作数就为1 + 'ab'子串的最大操作数，所以可以看到这是一个重叠子问题，那么理所当然的可以想到用动态规划来做，设dp[i]为从i开始的子串的最大操作数，dp[0]的值就是我们要求的s的最大操作数。
递推式为：
dp[i] = 1 + dp[i+len]      if s[i : i+len] == s[i+len : i+2*len]
dp[i] = 1            else
len为相同串长度，若有多个长度的相同串，dp[i]取最大值。

判断时间复杂度：
从后往前遍历s，对每个i计算dp[i]，每次计算dp[i]，len取[1, s.size / 2]。
每个dp[i]需要O($n^2$),计算n个dp[i]最后为O($n^3$),显然超了，所以还需要在判断相同串的方式上进行优化。

我们先计算任意两个子串间最长前缀和以便后续判断相同串，设lcp[i][j]为s[i : ]和s[j : ]的最长前缀和长度，它的递推式就为：

lcp [i] [j] = lcp [i+1] [j+1] + 1      if s[i] == s[j]
lcp [i] [j] = 0            else

有了lcp，两个子串是否相同直接看lcp就能得知。
判断时间复杂度：
计算lcp需要O($n^2$), 有了lcp计算每个dp[i]需要O($n$),计算n个dp[i]就为O($n^2$),所以最终的时间复杂度就为O($n^2$)。

代码

class Solution {
public:
    int deleteString(string s) {
        int dp[4005] = {};      //[i, n-1]串最大删除数
        //lcp[i][j]  s[i]与s[j]的最长前缀和
        vector<vector<int>> lcp(s.size() + 5, vector<int>(s.size() + 5, 0));
        for(int i = s.size() - 1;i >= 0;i--){
            for(int j = s.size() - 1;j > i;j--){
                lcp[i][j] = s[i] == s[j] ? lcp[i+1][j+1]+1 : 0;
            }
        }
        auto getmaxn = [&](int i)->int{
            int maxn = 0;
            int len = (s.size() - i) / 2;
            for(;len >= 1;len--){
                bool flag = true;
                if(lcp[i][i + len] >= len)
                    maxn = max(maxn, dp[i + len] + 1);
            }
            return maxn;
        };
        for(int i = s.size() - 1;i >= 0;i--){
            dp[i] = max(getmaxn(i), 1);
        }

        return dp[0];
    }
};

时间复杂度：$O(n^2)$
空间复杂度：$O(n^2)$

我的博客即将同步至腾讯云开发者社区，邀请大家一同入驻：https://cloud.tencent.com/developer/support-plan?invite_code=1ag9f3xrw54xw

最后修改：2022 年 12 月 16 日
© 允许规范转载
如果觉得我的文章对你有用，请随意赞赏