介绍
两个数进行异或运算,是依次比较两个数的二进制相同位的数,如果相同则该位结果为0,不同则该位结果为1.
比如5^7,比较方式如图
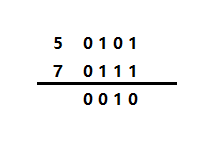
如果觉得相同为0不同为1不好记,也可以换一种记法,无进位相加,即让两数每一位都进行加法运算,但如果碰见两位都是1的情况,按加法的做法是结果为0再向前进一位,而异或就把这个进位舍弃掉即可。
性质
0^N == N
N^N == 0
异或满足交换律和结合律
交换律可以理解,那为什么异或满足结合律呢?我们不妨来看个例子,现在要计算9^3^7的结果,按照无进位加法的运算,就像加法一样,可以直接把三个数的二进制位对齐,然后一起算,再把进位的值舍去掉即可,算法如图:
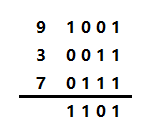
由此不难发现,计算每个进制位,当有奇数个1的时候,结果为1,当有偶数个1的时候,结果为0。由这个算法显而易见,交换运算数的顺序并不会影响结果,所以异或满足结合律。
应用
不用额外空间的情况下交换两个数字
比如要交换a和b的值,方法如下:
(注:如果a与b的值相同,交换后a与b都为0)
a = a^b;
b = a^b;
a = a^b;
原理:
当执行了第一条代码后,a的值变为a^b,
再执行第二条代码后,b的值变为a^b^b,由异或的结合律得a^b^b = a^(b^b),再由异或的性质N^N == 0得a^b^b = a^0,再由N^0 == N得a^b^b = a,所以此时b的结果就变为了a,
而执行第三行代码后,a = a^b^a,先交换再结合得a = b^0,然后由N^0 == N得a = b,即完成了a与b的值交换。
一个数组中有一个数出现了奇数次,其他的数都出现了偶数次,怎么找到这个数
解法:因为N^N等于0,0^0等于0,所以偶数个N做异或结果为0,又因为N^0=N,所以奇数个N做异或结果为N,所以这道题中,该数组所有数一起做异或,结果就为这个出现奇数次的数了。做法:定义一个变量初始为0,让这个变量依次对该数组的数做异或,最后的结果就是这个寻找的数。
一个数组中有两个数出现了奇数次,其他的数都出现了偶数次,怎么找到这两个数
假设这两个数为a与b,那么该数组所有数一起做异或结果为a^b,再来观察题目,因为两个数出现奇数次,所以a肯定不等于b,那么在它们的二进制位中,至少有一位,a与b的该位值不同,找到这一个进制位,把数组中所有数根据这个进制位的值为1还是0分为两部分,那么,首先a与b一定不会在同一部分,其次不会有相同的数在不同部分,那么我再定义一个变量对其中一部分所有数做异或,结果肯定为其中一个出现了奇数次的数,再让这个变量对之前结果为a^b的变量做异或,结果就肯定为另一个奇数次的数了。